9주차-Activations, Implementation Details of Neural Network

• Choosing Activation Function for Output Layer

 

- Sigmoid: Binary Classification 문제에서 사용
- Linear: Regression 문제
- ReLU: Hidden Layer층에서 주로 사용, 음수값 제거 
- Tanh: 양수와 음수를 모두 고려

 

• Choosing Activation Functions for Hidden Layer

- Sigmoid: 출력값이 확률값을 나타낼 때 사용
- ReLU: 효율성과 간단함, 음수값 제거
- Leaky ReLU: 음수값을 제거하지 않고 작은 기울기를 부여
- GELU: Gaussian 분포를 따르는 Activation Funtion

 

• Why Nonlinear Activation Function

- Linear Function만 사용할 경우, 모델은 복잡하게 분류하거나 학습할 수 없다.
- Nonlinear Function을 사용하면, 데이터 공간을 비선형적으로 mapping하여 신경망이 복잡한 데이터 패턴을 학습 가능

 

• Vanishing Gradient

• Sigmoid Activation Fuction

• ReLU Activation Function

 

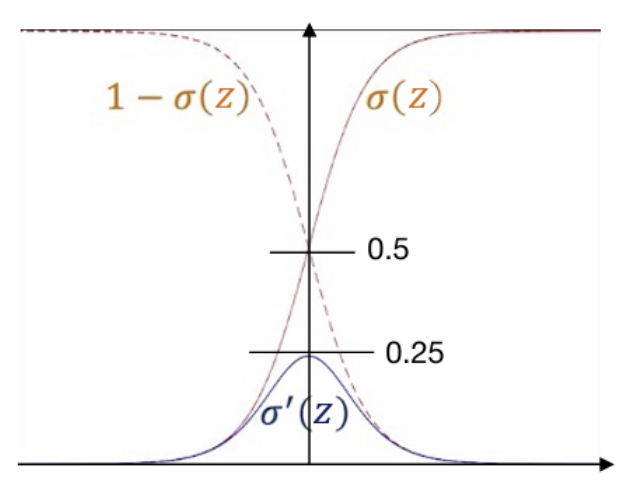
# Recap) Sigmoid Function의 도함수

 

 

---

Implementation Details of Neural Network

• Update Rule for Neural Network

 

• Implementation (Using Class)

 

• __init__

- weight W와 b를 초기화한다.

self.w = ~
self.b = ~​

• forward

- Input data X를 기반으로 출력값을 계산하는 과정

z1 = self.w @ X + self.b1
a1 = self.sigmoid(z1)​

 

• update

- Backpropagation을 포함하여 weight와 bias를 update

# lr : 학습률(Learning Rate)
# y : 실제값
# x: 입력 데이터

def sigmoid(self, z):
	return 1/(1 + np.exp(-z))​

 

• Implementation (__init__)

• 초기화 과정

1. W 초기화

self.w1 = np.random.rand(3, 4)​

- 첫 번째 층에서 입력층(4)과 첫 번째 은닉층(3)을 연결하는 가중치 행렬 W1

2. Bias 초기화

self.b1 = np.zeros(3, 1)

- 첫 번째 은닉층(3)에 대한 Bias 초기화

3. 구조 정의

EX) cf = [4, 3, 2, 1]

# cf[1]: 첫 번째 은닉층의 뉴런수 (3)
# cf[2]: 두 번째 은닉층의 뉴런수 (2)

 

• Implementation (Forward)

- broadcasting: 각 입력 데이터에 동일하게 적용되도록 크기를 자동 확장

 

• Implementation (Forward Propagation)

• forward(self, x)

- X: 입력 데이터
- 입력 값 X를 기반으로 Forward Propagation을 수행하고, 각 층의 z[l] 및 a[l] 값을 update

• code 설명

self.z1 = np.matmul(self.w1, X) + self.b1
self.z1 = self.w1 @ X + self.b1

=> np.matmul: 행렬 곱셈

self.a1 = self.sigmoid(self.z1)

=> a[l] = g(z[l]), g: activation function(Sigmoid)

 

• Implementation (Backpropagation)

• 최종 출력층 δ

• Hidden Layer δ

• Backpropagation 행렬 연산

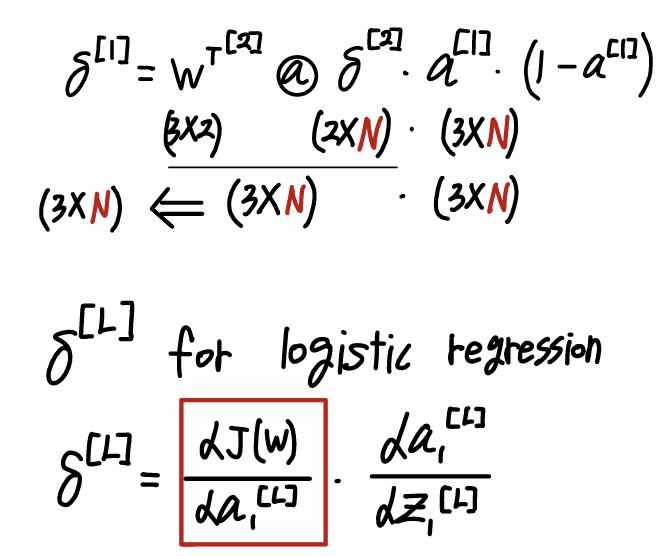
• Logistic Regression

• Weight update