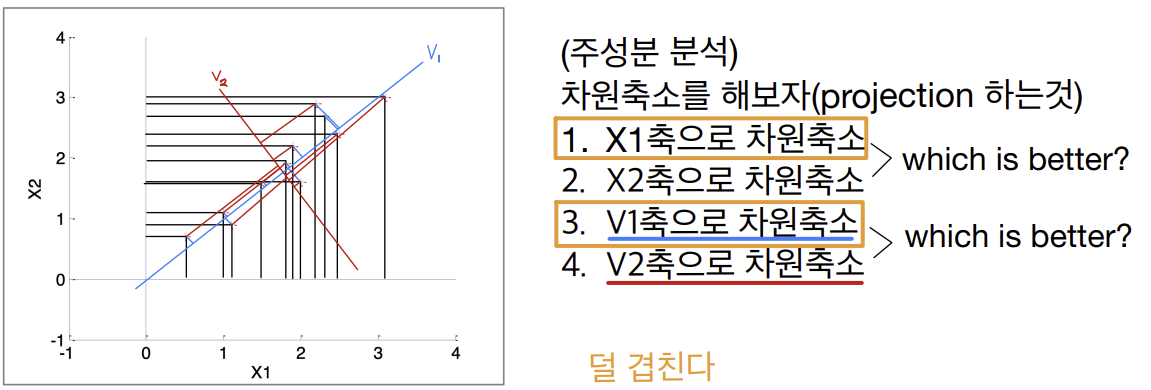
12주차-Principal Component Analysis

 

 

• Eigenvalue(고유값) & Eigenvector(고유벡터)

정방행렬 A에 대하여 Ax = λx  (상수 λ) 가 성립하는 0이 아닌 벡터 x가 존재할 때 상수 λ 를 행렬 A의 고유값 (eigenvalue), x 를 이에 대응하는 고유벡터 (eigenvector) 라고 합니다.  

 

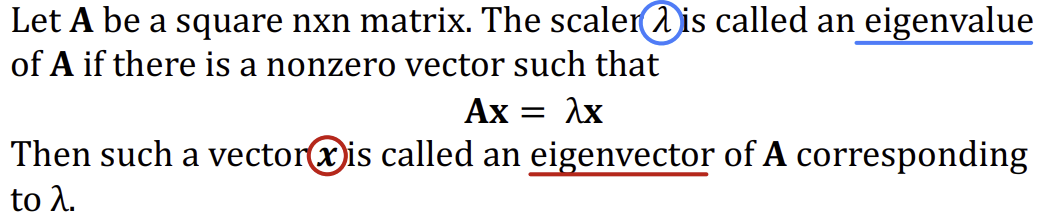
EX)

 

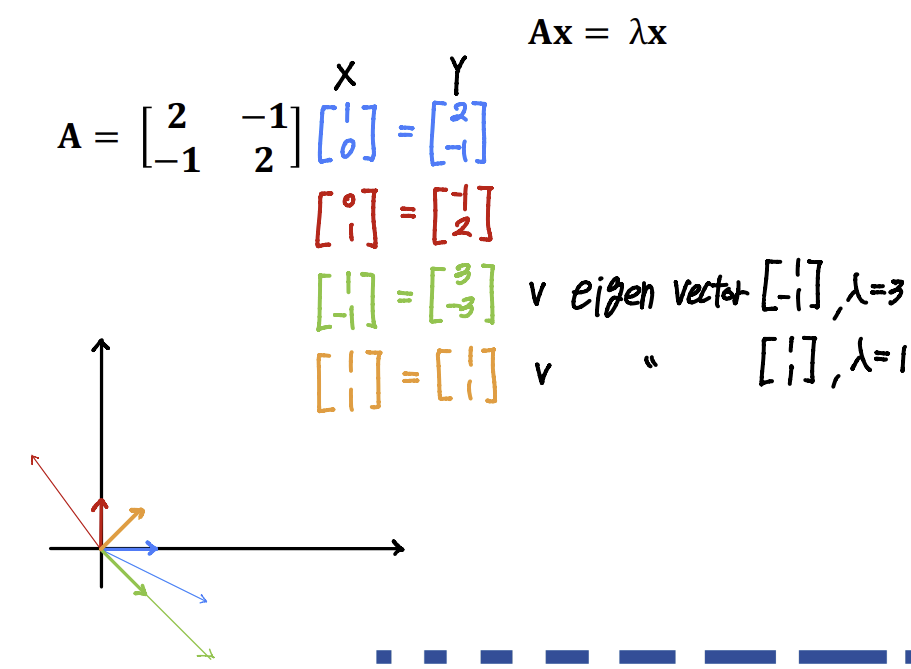
• Non-trivial solution(비자명해)

 

EX)

 

 

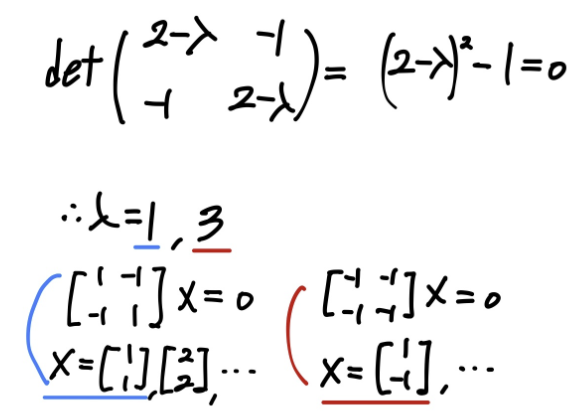
• Eigendecomposition(고유값 분해)

 

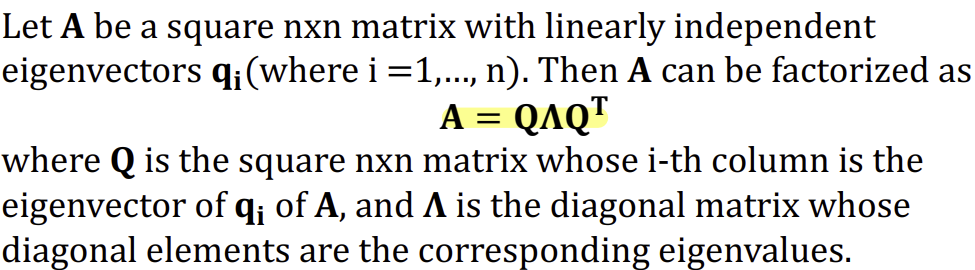
Q) 모든 eigenvectors가 서로 orthogonal한가?

A) A가 서로 symmetric(대칭)한 경우 yes!

 

EX)

 

• Usecase of Eigendecomposition

 

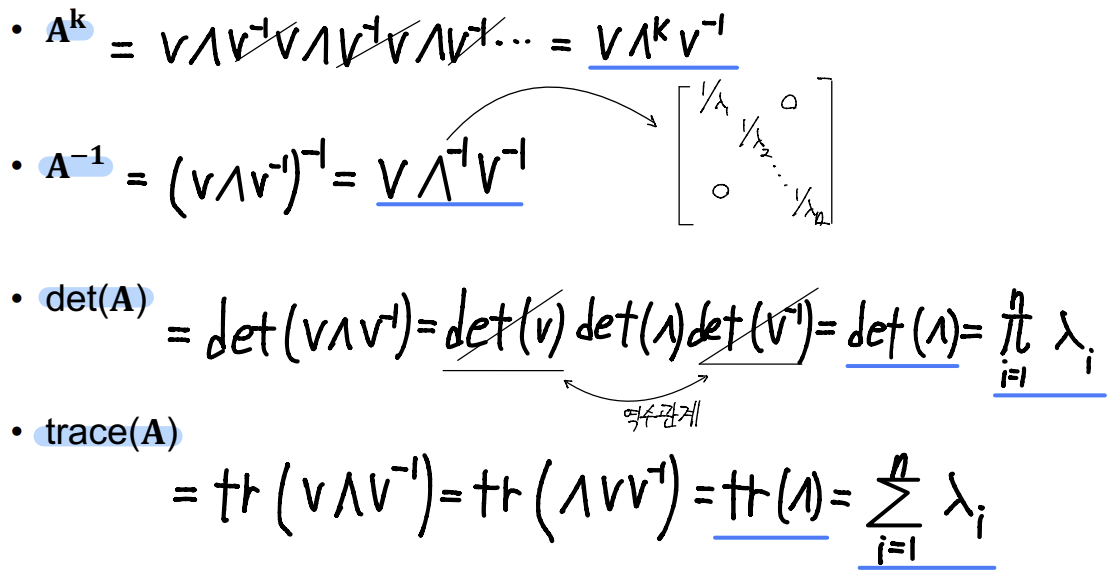
• Eigendecomposition for Symmetric matrix(대각행렬)

 

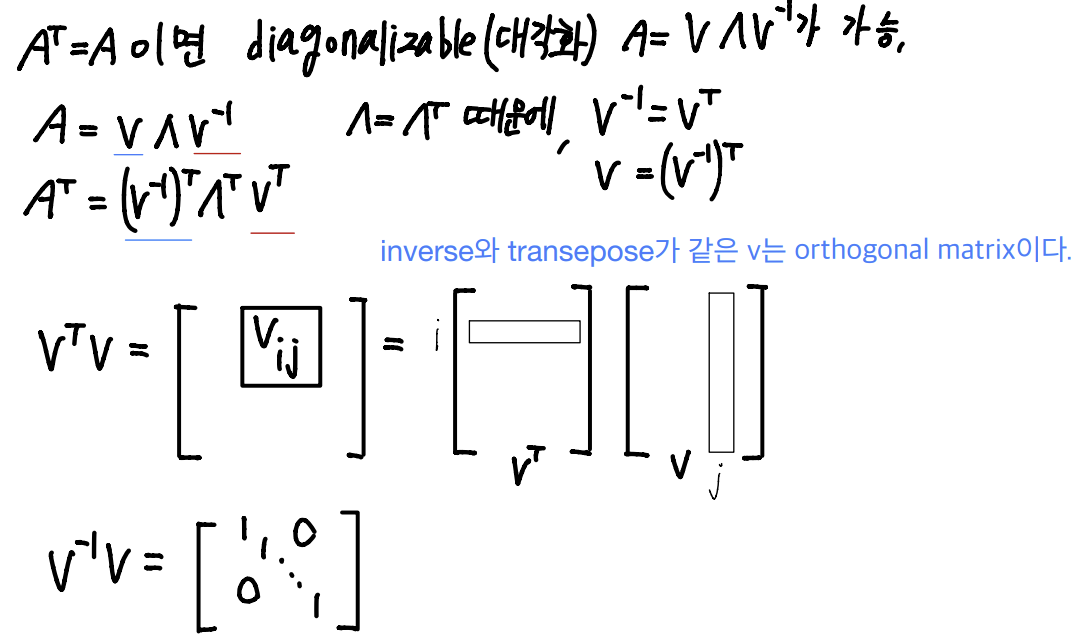
EX) A는 3X3 symmetric matirx

 

• Geometrical Analysis

 

 

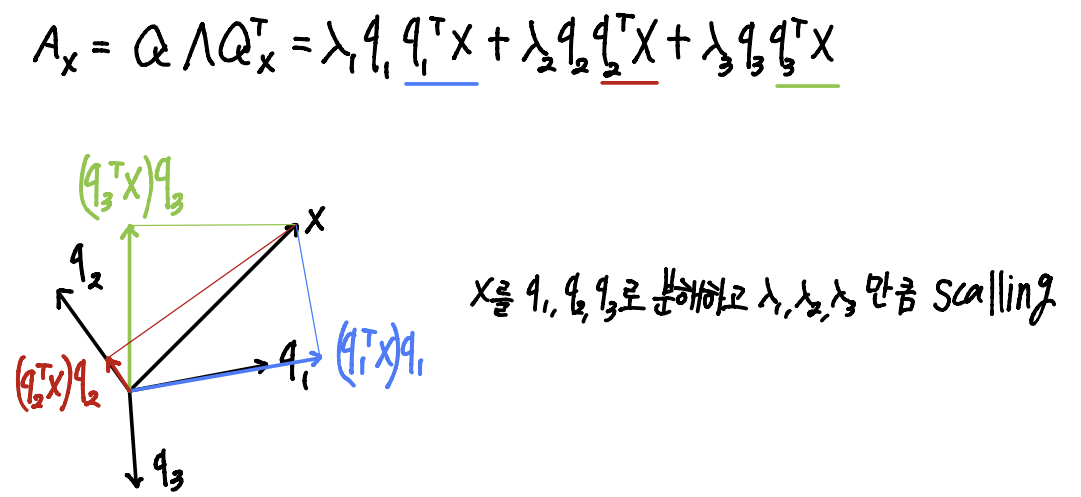
• Principal Component Analysis(PCA)