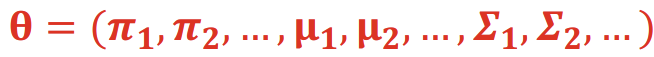- MAP(Maximun a posterior): 사후확률
주어진 데이터와 사전 정보(prior information)를 모두 고려하여 사후 확률(posterior probability)을 최대화하는 파라미터 값을 찾는 방법.

데이터 D가 주어졌을 때 가설 h의 사후 확률.

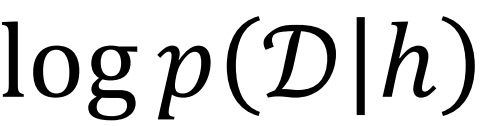

- MLE(Maximun Likelihood Estimate): 우도예측
주어진 데이터가 관찰될 확률을 최대화하는 파라미터 값을 찾는 방법.

likelihood 항은 데이터의 양 N에 따라 지수적으로 증가하고, 사전 확률은 일정하게 유지된다.
=> 데이터가 많아질수록 MAP추정은 MLE추정에 수렴하게 된다.
즉, 충분한 데이터가 있는 경우, 데이터는 사전 확률(prior)의 영향을 압도하게 된다.
- 정리
| MAP | 사전 확률을 고려하여 최대화 |
| MLE | 사전 확률을 고려하지 않음 |
=> 데이터가 많아질수록 MAP는 MLE에 수렴한다.

=> p(h) (prior: 사전확률)가 균등 분포에서 나왔다면, MAP추정은 MLE추정과 동일하다.
- Basyesian Concept Learning

- parameter vector setha

- MLE는 예측단계(prediction phase)가 아니라 학습단계(training phase)에 적용된다.

- Linear Regression w/ Gaussian Distribution Likelihood

주어진 데이터셋 D에 대해 모델 또는 파라미터 θ를 결정해야 한다.
- Gaussian분포를 사용하는 Linear Regression
- 모델 형태


- 주어진 데이터셋 D에 대해 모델 파라미터 θ를 결정

- 파라미터 θ를 추정하는 일반적인 방법은 MLE를 계산하는 것

- 훈련 예제가 독립적으로 동일한 분포를 따른다고 가정하는 것이 일반적. log-likelihood는

- Deriving MLE
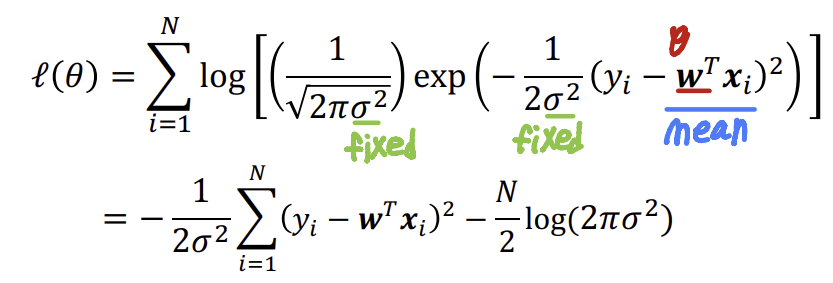
위 과정은 MSE와 동일한 결과를 도출한다.

- Revisit Minimizing MSE


- Log-likelihood(NLL)

NLL(음의 로그 우도)를 최소화하는 것은 MLE와 동등하다.
- Overfitting
예측 모델 또는 머신 러닝 모델이 학습 데이터에 너무 밀접하게 맞춰져서 새로운 데이터에 대한 예측 성능이 떨어지는 현상
MAP와 비교했을 때 MLE의 한계로 지적되는 점이다.
=> MLE는 과적합의 위험이 더 크다.
- Solution for Overfitting => MAP or Abundant Data
1. 많은 데이터가 overfitting 방지
2. MAP
- Regression training에서 Posterior공식

- 지금까지 p(w)가 균등 분포를 따른다고 가정했다. 즉, w가 균등 확률 분포를 따른다고 가정했다.
- "w의 흔들림(wiggle)"을 줄이기 위해, 사전 확률 p(w가 평균이 0인 가우시안 분포를 따른다고 가정할 수 있다:

(τ2는 사전 분포의 강도를 조절)
overfitting 문제를 해결하기 위해 사전 확률을 가우시안 분포로 설정하는 MAP 추정 방법을 설명하고 있다.
이를 통해 모델의 복잡도를 조절하고 overfitting을 방지할 수 있습니다.
- Performing MAP
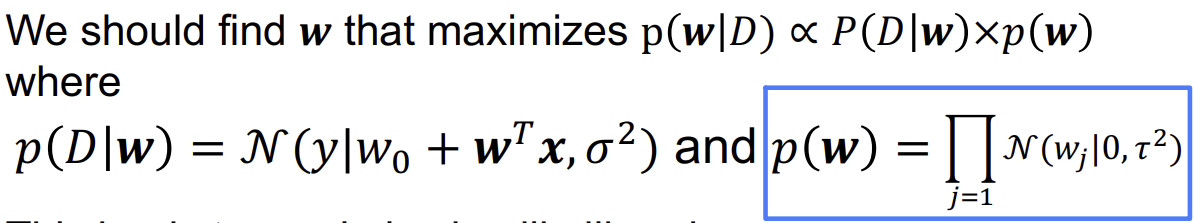
- 이는 log-likelihood를 최대화하는 것으로 이어진다.

- 이는 다음을 최소화하는 것과 같다.
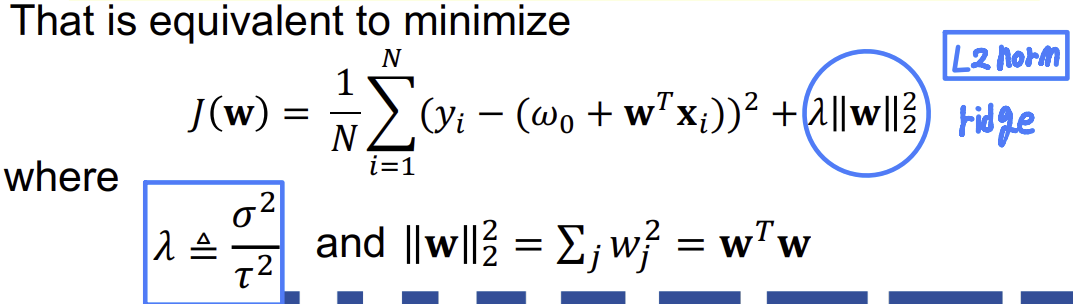
- Supervied(지도학습): 입력(x)과 출력(y) 쌍을 이용해 학습한다.
- UnSupervised: 입력데이터만 주어진다.
Clustering: 대표적인 Unsupervised learning 알고리즘

- K-means Clustering
1. 초기 클러스터 중심을 임의로 설정하고, 각 데이터 포인트를 가장 가까운 클러스터 중심에 할당한다.
2. 클러스터 중심을 각 클러스터의 평균으로 업데이트하고, 데이터 포인트 할당을 반복한다.
3. 클러스터링 결과가 더 이상 변하지 않을 때까지 이 과정을 반복한다.
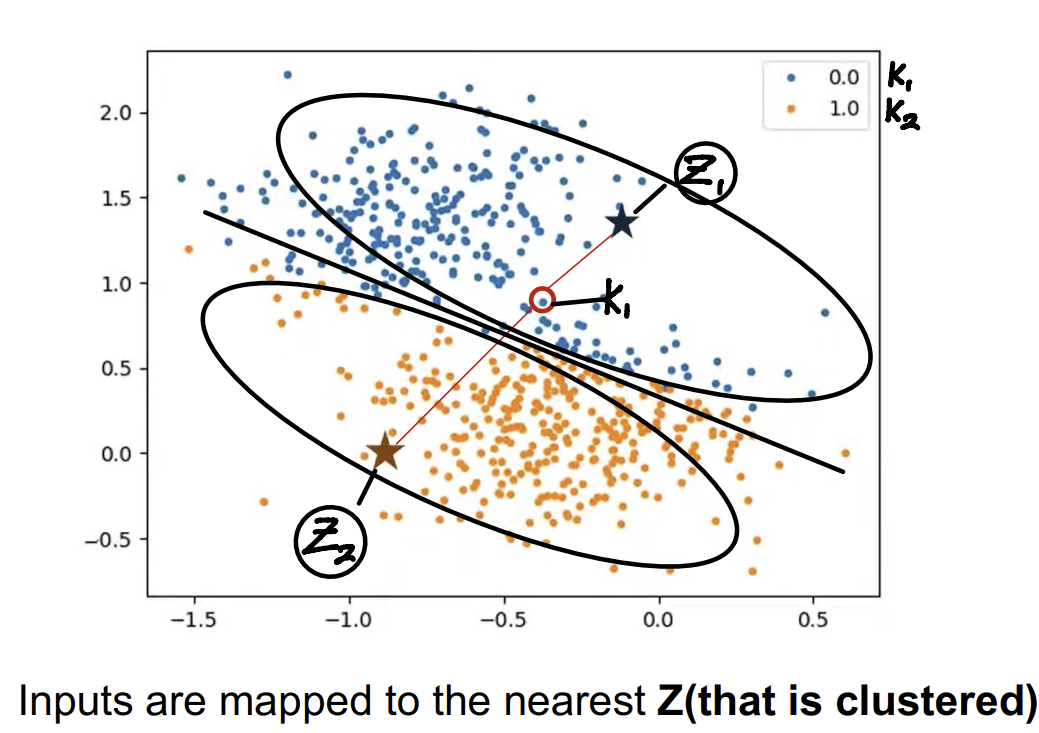
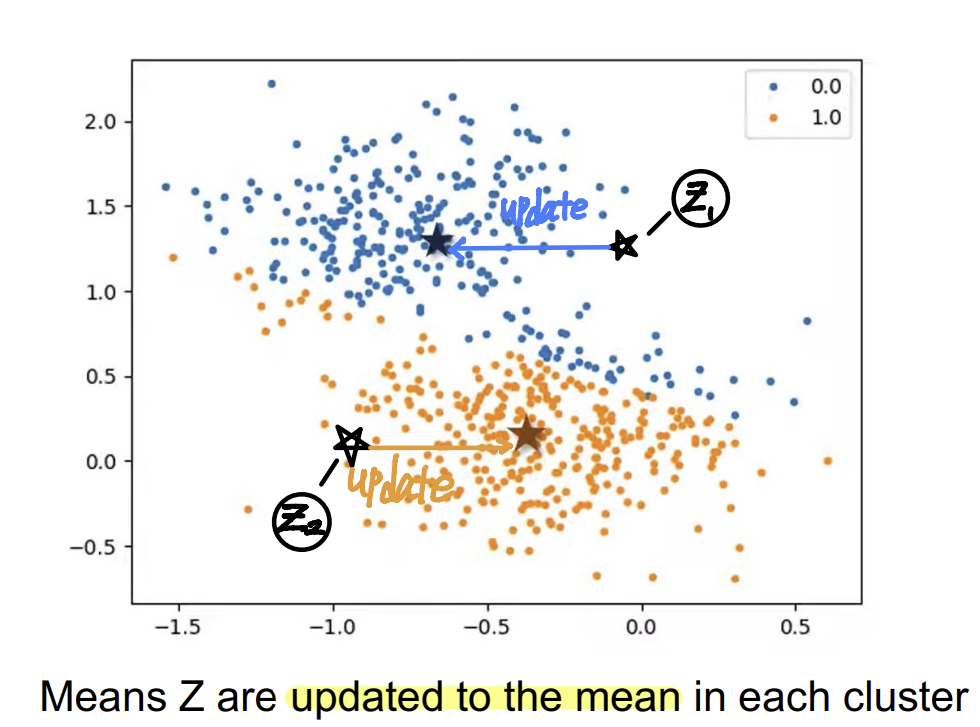


- k-Medoids
k-clustering은 이상치(outlier)에 약하다.
=> k-Medoids를 사용하여 이상치의 영향을 줄일 수 있다.

- Binomial distribution(이항분포)
N: 시행횟수/ P: 확률

- Bernoulli distribution(베르누이 분포)
- Multinomial distribution(다항분포)

- Categorial distribution(범주형 분포)
- covariance matrix(공분산 행렬)
각 특징(feature)들 간에 상관 관계를 나타냄.

- Correlation coefficient(상관계수)

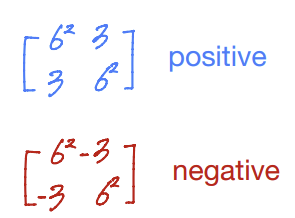
- The Multivariate Gaussian(다변량 가우시안 분포)



- Mixture model(혼합모델)

- Gaussian Mixture Model(GMM)

우리는 GMM 클러스터링에서 파라미터 θ를 결정해야 한다.
θ는 다음과 같이 구성된다.우리는 잠재 변수를 "책임도(responsibility)" 로 정의하며, 이는 다음과 같이 업데이트된다.
- rik를 결정하는 방법은?
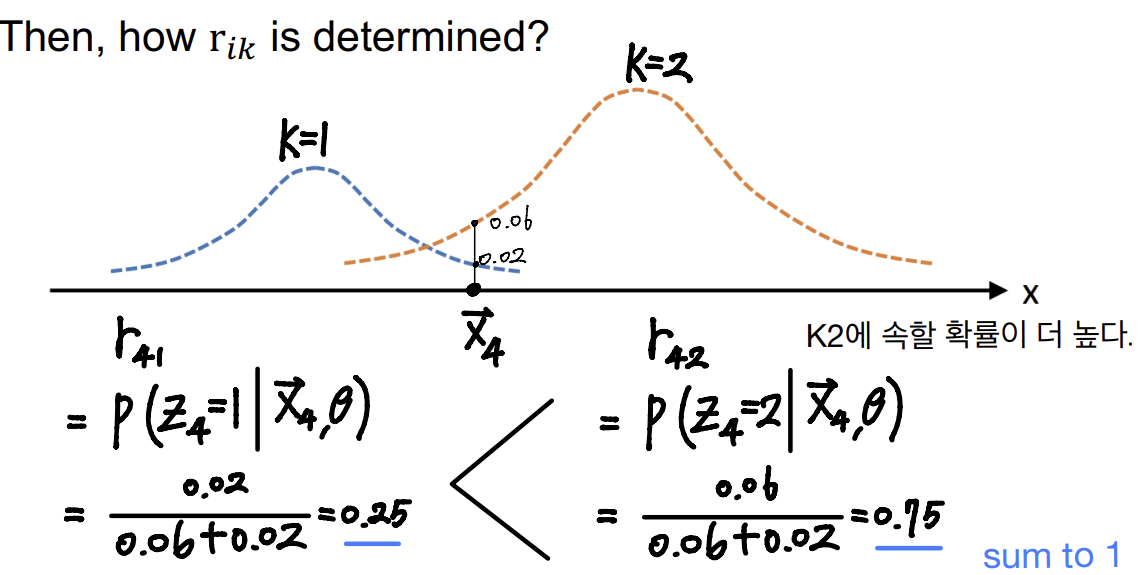
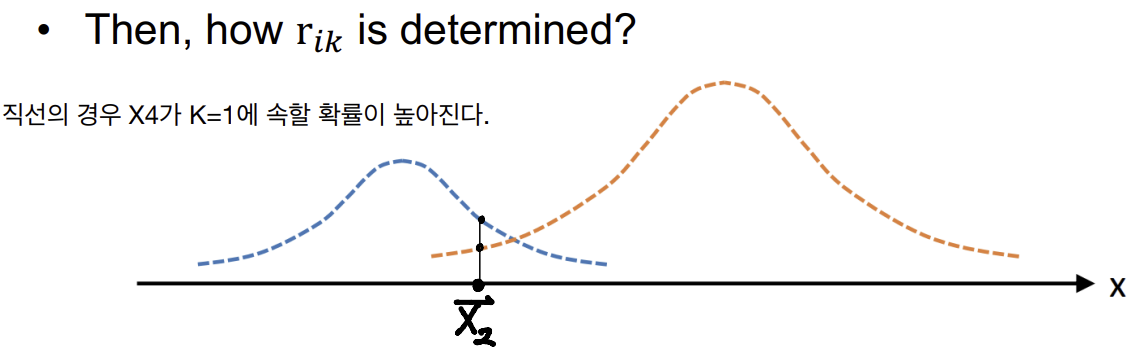
- Soft clustering
각 데이터 포인트가 여러 클러스터에 속할 확률을 가진다.

- Hard clustering
각 데이터 포인트가 정확히 하나의 클러스터에 할당된다.

- 를 개선하는 방법
업데이트

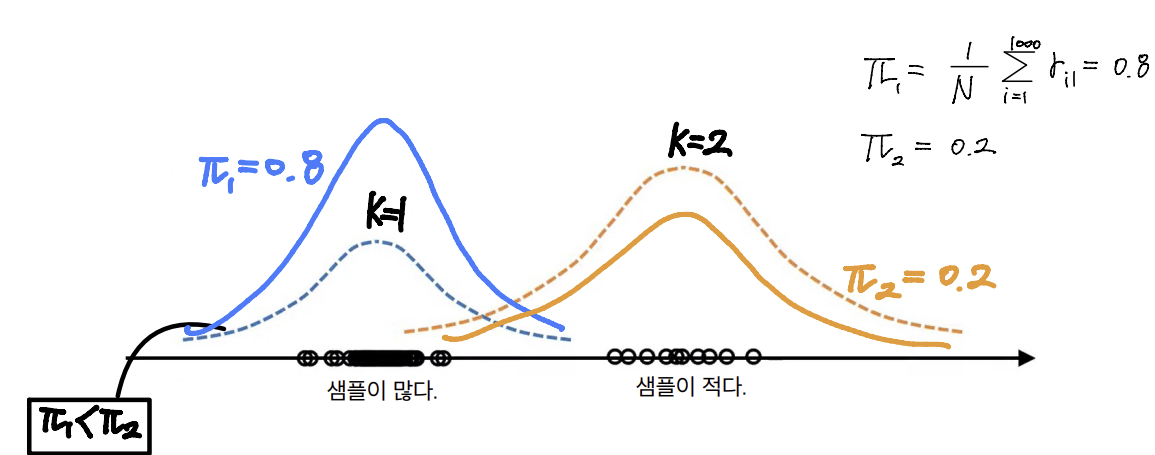
- GMM을 사용한 Hard clustering

- EM algorithm
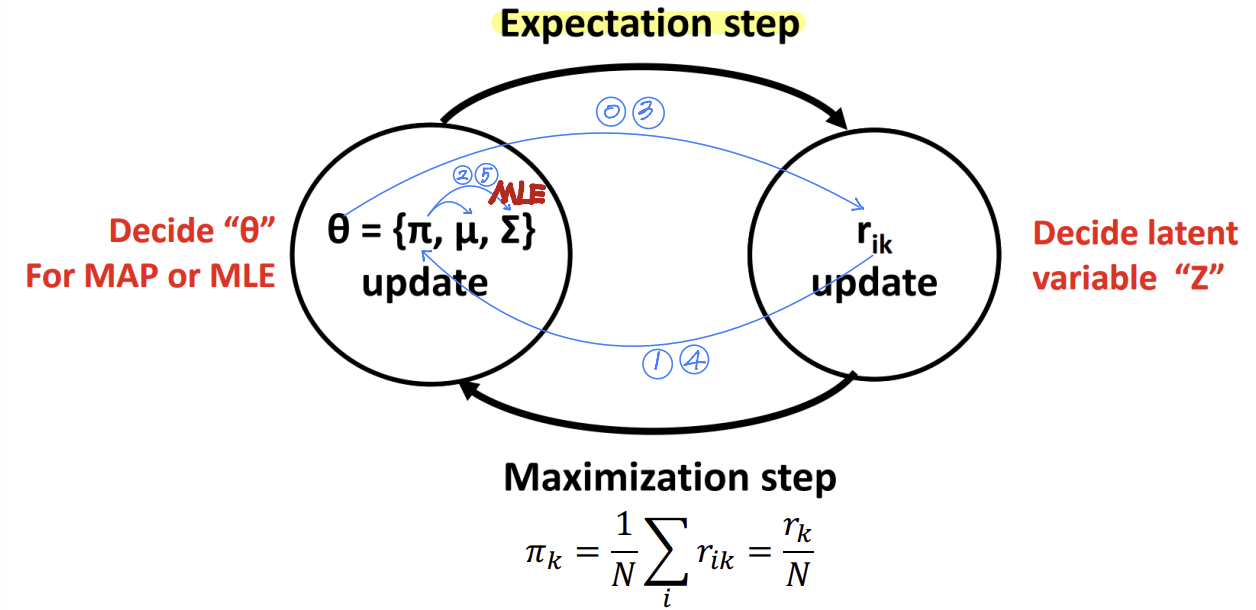
1. Expectation step: 현재 추정된 파라미터 θ를 사용하여 각 데이터 포인트 xi가 각 클러스터 k에 속할 책임도 rik를 계산
=> rik는 다음과 같이 계산

2. Maximization step: 책임도 rik를 사용하여 파라미터 θ={π,μ,Σ}를 업데이트

3. 반복 과정: 기대단계, 최대화 단계는 반복적으로 수행
=> 각 반복에서 파라미터 θ는 점점 더 정확해진다.
=> 알고리즘이 수렴(convergence)할 때까지 계속
'3-1 > Data Mining' 카테고리의 다른 글
| 13주차-Probability & MLE, MAP (1) | 2024.06.07 |
|---|---|
| 12주차-Principal Component Analysis (2) | 2024.06.02 |
| 10주차-AdaBoost & GBM (1) | 2024.05.12 |
| 9주차-SVM(2) (0) | 2024.05.11 |
| 7주차-SVM(1) (1) | 2024.05.11 |