- Knowledgw Distillation
- "지식을 증류한다"라는 의미
- 상대적으로 성능이 뛰어나고 용량이 큰 모델(teacher)에서 상대적으로 용량이 작은 모델(student)로 지식을 추출하는 방법
- Cross Entropy & Entropy
p: 실제 확률 분포 / q: 모델의 예측 확률 분포
<Cross Entropy> H(p, q)<Entropy> H(p)
EX)
- KL Divergence(Kullback-Leibler divergence)(KL div)
- 두 확률 분포 p와 q간의 차이를 측정하는 방법
<성질>
1. 비음수성- 두 분포가 같을 때만 0이 된다.
2. 비대칭성- KL div는 대칭적이지 않다.
<KL div Loss>
- Soft Label
- Hard Label
- 정확한 클래스에만 확률 1을 할당하고 나머지 클래스에는 0을 할당하는 one-hot vector
EX)

- Soft Label
- 모든 클래스에 대해 확률을 부드럽게 할당
- 주요 클래스에 높은 확률을 주고, 다른 클래스에도 아주 작은 확률을 준다
EX)

- Label Smoothing
- Hard Label을 Soft Label로 변환하는 기법
- 과적합 방지와 모델의 일반화 성능 향상에 도움을 준다.
EX)

- Softmax with Temperature

- Hilton's KD
- 성능이 뛰어난 Teacher 모델에서 간결하고 작은 Student 모델로 지식을 전이하는 기법

<Teacher 모델>
- 복잡하고 큰 모델
- Softmax with Temperature을 사용하여 yhatT를 생성
- Teacher 모델은 학습이 완료된 상태, 업데이트 되지 않고 Freeze된다!
<Student 모델>
- 간결하고 작은 모델
- 입력 x를 받아 softmax를 적용하여 예측 확률 분포 yhatS를 생성
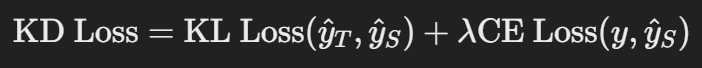
Weight Initialization
- Initialization Matter

<convex>
- 초기 weight w0가 어디에 위치하든, 최적의 지점으로 수렴
- 초기화가 크게 중요하지 않다.
<non-convex>
- 초기 weight w0가 어디에 위치하느냐에 따라 학습 결과가 달라진다.
- 잘못된 초기화는 로컬 최소점에 갇혀버린다.
- Zero Initialization
- 모든 가중치를 0으로 초기화한다.
- 모든 뉴련이 동일한 값을 학습하게 되어 서로 다른 뉴런 간에 차별화가 불가능
- Constant Initialization
- 모든 가중치를 같은 상수 값으로 초기화한다.
- 모든 뉴련이 동일한 값으로 계산하므로 서로 다른 뉴런 간에 차별화가 어렵다(대칭 문제)
- Random Initialization
- 가중치를 무작위로 초기화한다.
- 각 뉴런이 서로 다른 값을 학습하게 되어 다양한 특징을 학습 가능(대칭성 문제 해결)
- Initialization Tip
- Weight
- 무작위로 초기화해야 대칭을 깨뜨릴 수 있다.
- 0으로 초기화하면 기울기가 0이되어 학습이 제대로 이루어지지 않는다.
=> Small uniform 또는 Gaussian Values를 사용하는 것이 좋다.
- Bais
- Bias는 0으로 초기화
- ReLU 활성화 함수의 경우, bias를 작은 양수 로 초기화하면 dying ReLU 문제를 해결하는데 도움이 된다.
- Xavier Intialization
- Sigmoid 또는 Tanh 같은 활성화 함수에서 훈련을 안정화하기 위해 설계
- 모든 층의 입력이 균등하게 분포되도록 보장
- He Intialization
- ReLU 활성화 함수에 최적화되어 있다.
- ReLU는 음수 입력에 대해 비활성화되기 때문에, He Intialization은 입력 뉴런의 수에 맞춰 가중치를 초기화
Learning Rate Decay
- Intuition of learning rate decay

- Learning rate drop: 학습률이 줄어들수록 경로가 더 부드럽고 안정적으로 최적점으로 수렴
- Learning rate decay

<Learning rate decay>
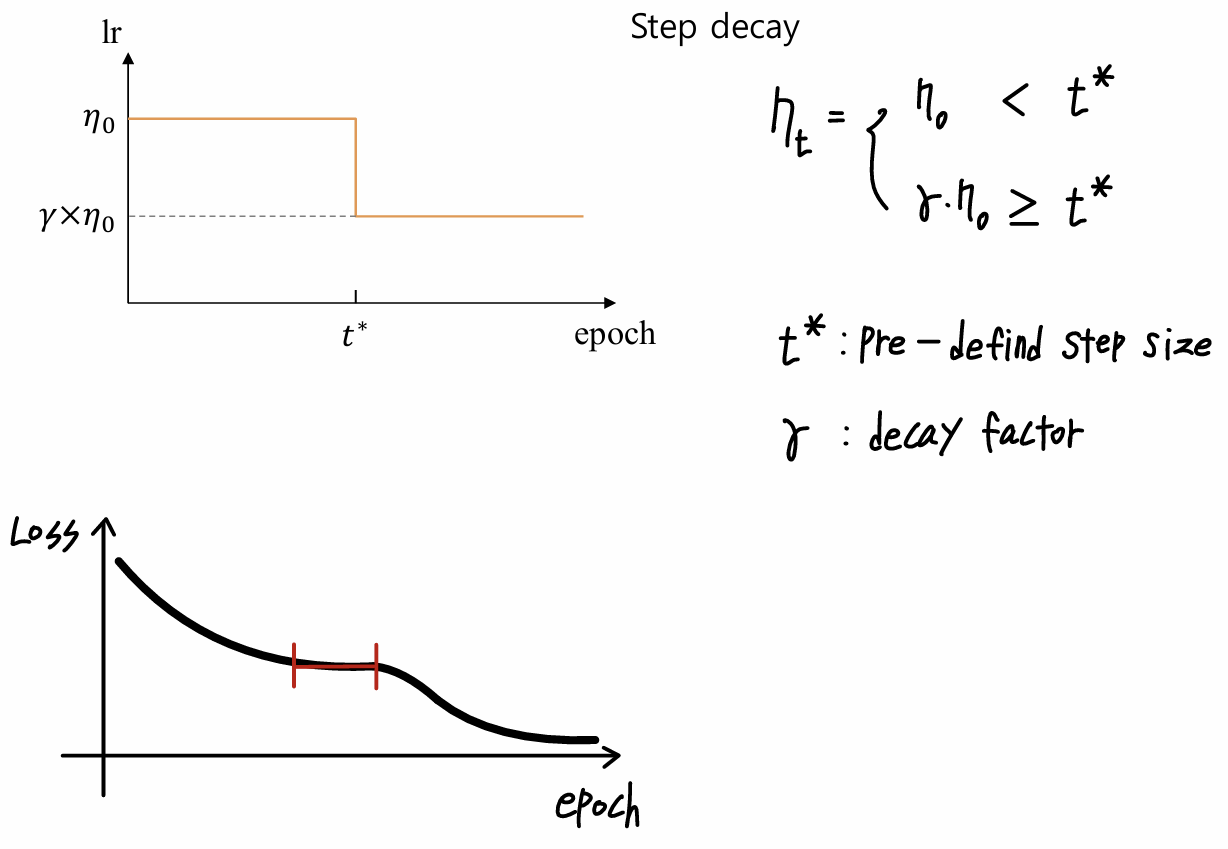
<Step Decay>
- t*: 미리 정의된 step size로 학습률이 감소하는 시점을 나타냄
- Γ: 감소 계수로, 학습률을 얼마나 줄일지 결

<Exponential Decay><Cosine Decay>
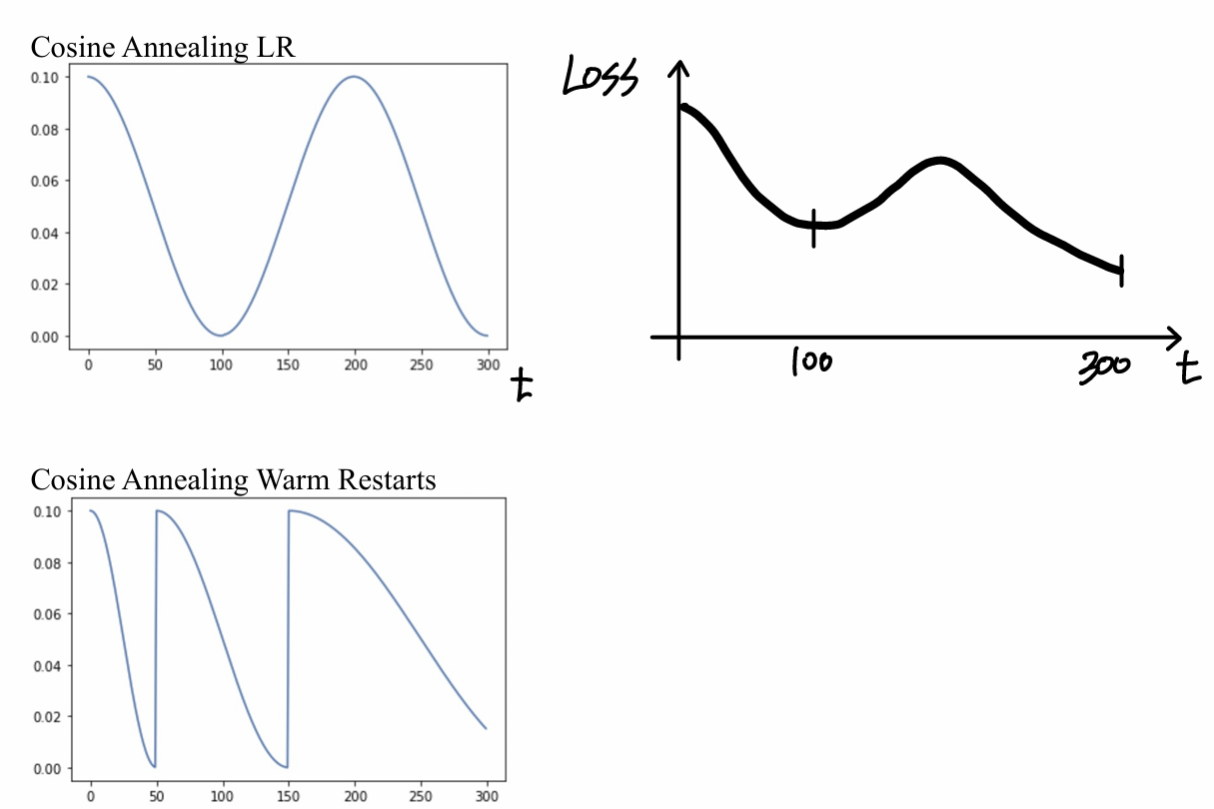
- Cyclic Learning Rate
Batch Normalization
- Motivate for Batch Normalization
- Input Scaling
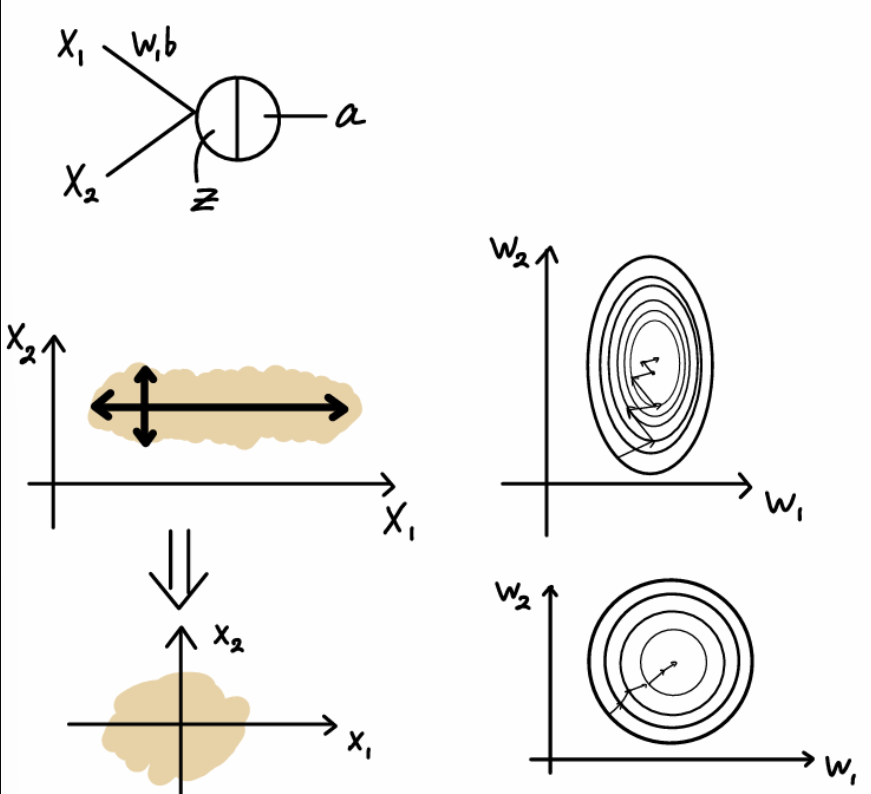
-입력 데이터가 Scaling되지 않아 X2의 값 범위가 좁고 X1의 값 범위는 넓다.
=> 가중치 공간에서 최적화 경로가 비효율적으로 왜곡
- 데이터가 Scaling된 후, 두 입력 차원의 분포가 더 균일
=> 입력 데이터가 정규화된 후, 가중치 공간에서 최적화 경로가 더 단순하고 효율적이 된다.
- Standard Scaler

- Activation Normalization
- Batch Normalization for Training
=> Γ, β are learnable parameters
- Batchnorm을 적용하는 경우 bias생략
- Batch Normalization for Test(Inference time)
- Using M, σ from training phase
Dropout
- Dropout
- Overfitting을 방지하기 위한 정규화 기법
- 훈령과정에서 일부 뉴런을 무작위로 비활성화하여 모델이 특정 뉴런에 과도하게 의존하지 않도록 돕는다.
'3-2 > 기계학습' 카테고리의 다른 글
| 11주차-Loss Function Design (0) | 2024.12.07 |
|---|---|
| 10주차-Multi-class Classification (1) | 2024.12.01 |
| 9주차-Activations, Implementation Details of Neural Network (1) | 2024.11.27 |
| 8주차-Neural Network (0) | 2024.11.27 |
| 7주차-Regularization (2) | 2024.10.27 |
















