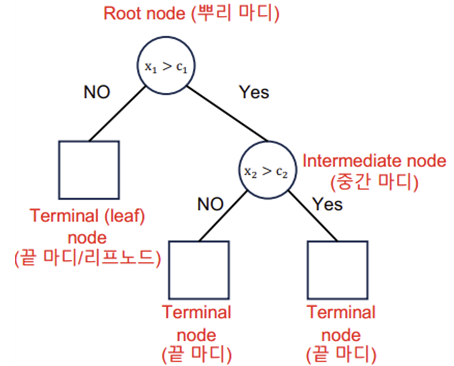
Decision Tree (의사결정나무): 데이터에 내제되어 있는 패턴을 변수의 종합으로 나타내는 예측/ 분류 모델을 Tree형태로 만든 것
Data => Algorithm => Model(Output)
->데이터를 2개 혹은 그 이상의 부분집합으로 분할 (데이터가 균일해지록 분할)
->분류(Classification): 비슷한 범주(impurity낮다)를 갖고 있는 관측치끼리 모음
->예측(Regression): 비슷한 수치(분산 낮다)를 갖고 있는 관측치끼리 모음
->끝마디의 수만큼의 분류 규칙을 가진다.
-Regression Tree

-> Leaf node: 5개
-> 데이터를 m개로 분할
-> 최상의 분할은 다음 비용함수(cost function)를 최소로 할 때 얻어짐
-> 각 분할에 있는 y값들의 평균으로 예측했을 때 오류가 최소
회귀 모형에서 불순도를 측정하는 과정 (분산이 낮은 것을 pure하다고 봄)
-> 불순도(Impurity)측정
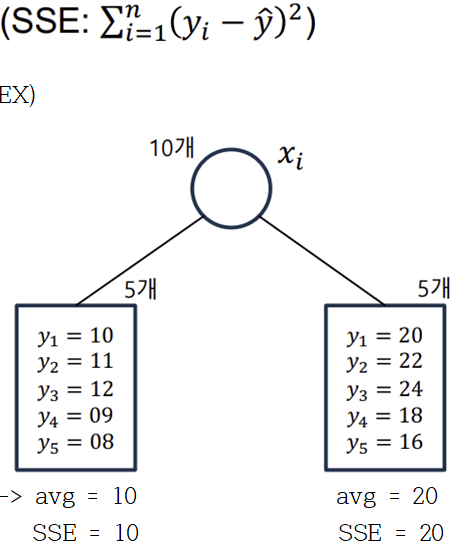
=> SSE가 낮은 것을 선택
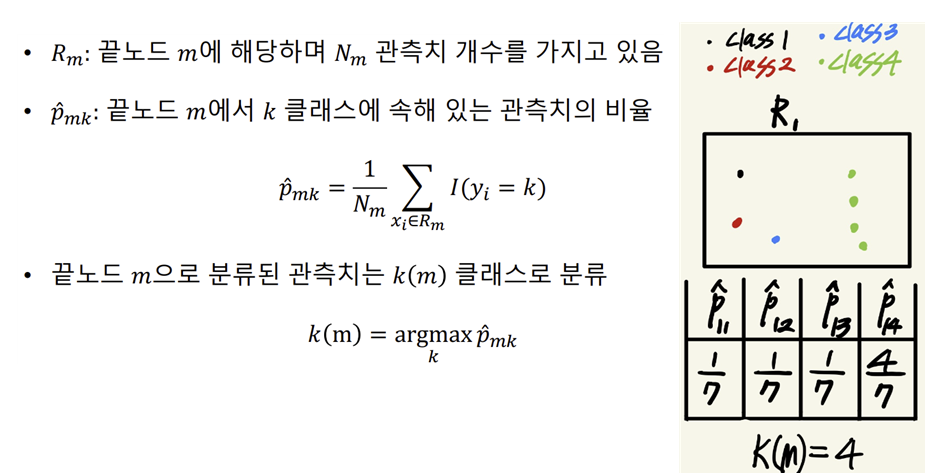
-Classifier Tree
-> 분할변수와 분할 기준은 목표변수의 분포를 가장 잘 구별해주는 쪽으로 정한다.
-> 목표변수와 분포를 구별해주는 측도로 entropy 또는 impurity를 정의
EX) 클래스0(45%), 클래스1(55%)인 node는 각 클래스의 비율이 (90%), (10%)인 node에 비해 impurity가 높다.
-> 각 node에서 entropy 또는 impurity가 최대로 감소하도록 선택
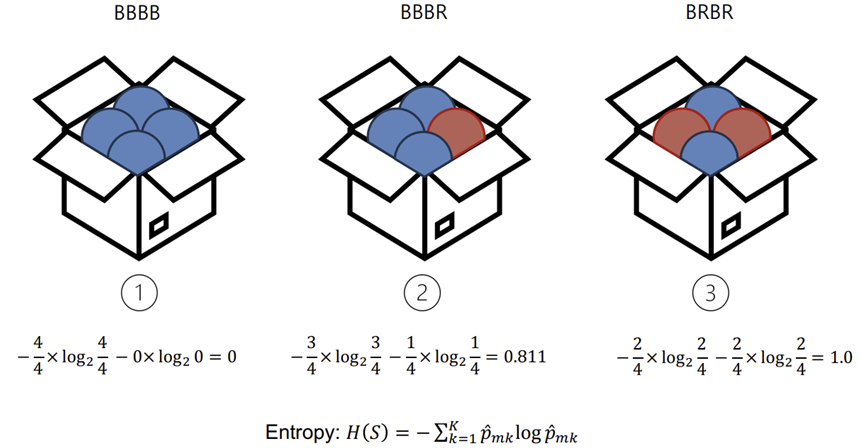
*Impurity

*Entropy (정보량 적다 = Entropy낮다)
-IG(S,A) (Information Gain): 데이터를 나누었을 때 줄어든 엔트로피의 양
-> S: 데이터 표본, A: 나눈 부분들의 집합/ 높을수록 GOOD!

EX)


-Gini-index
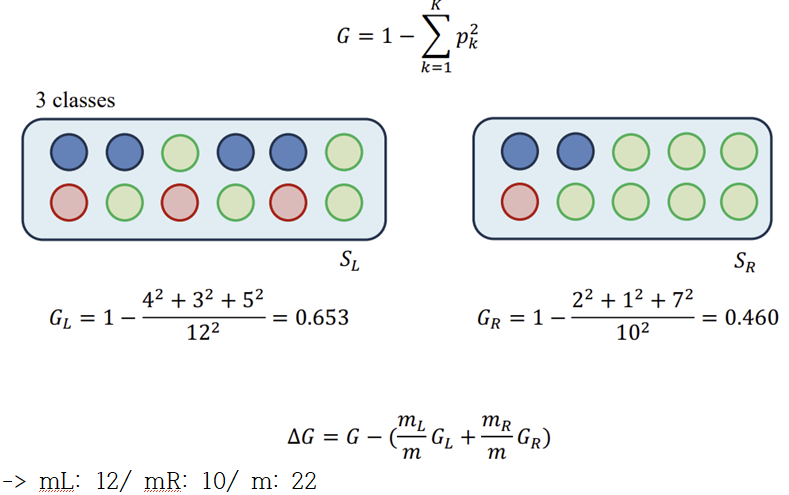

-Disadvantages of Decision Tree
1) 계층적 구조로 인해 중간에 error발생하면 다음 단계로 error가 계속 전파
2) 학습 데이터의 미세한 변동에도 최종 결과 크게 영향
3) 적은 개수의 노이즈에도 크게 영향
4) Tree의 최종노드 개수를 늘리면 overfitting위험(Low Bias, Large Variance)
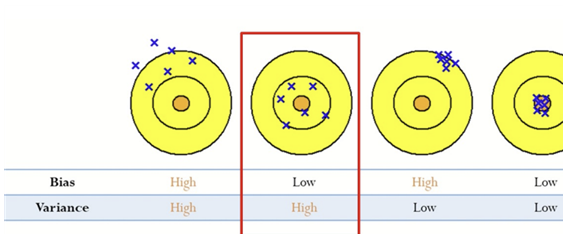
-> 해결 방안 = 랜덤 포레스트
-min_samples_leaf: 리프노드가 되기 위해 필요한 최소 샘플수
-max_leaf_nodes: 트리가 가질 수 있는 리프노드의 최대 수
-max_depth: 트리의 최대 깊이
'3-1 > Data Mining' 카테고리의 다른 글
| 7주차-SVM(1) (2) | 2024.05.11 |
|---|---|
| 6주차-Random Forest (0) | 2024.05.11 |
| 4주차-Linear Models (1) | 2024.05.11 |
| 3주차-K Nearest Neighbors (0) | 2024.05.11 |
| 2주차-Supervised Learning (1) | 2024.05.11 |