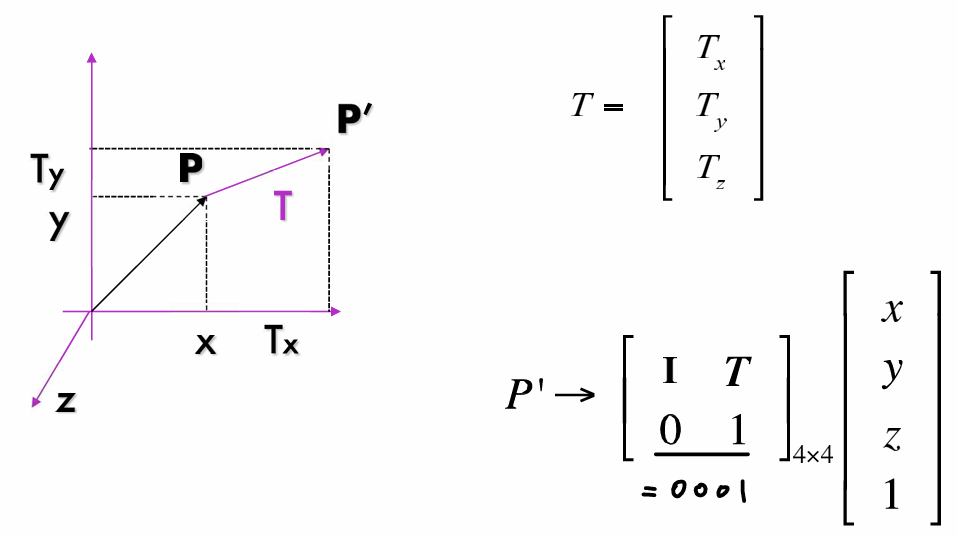REVIEW
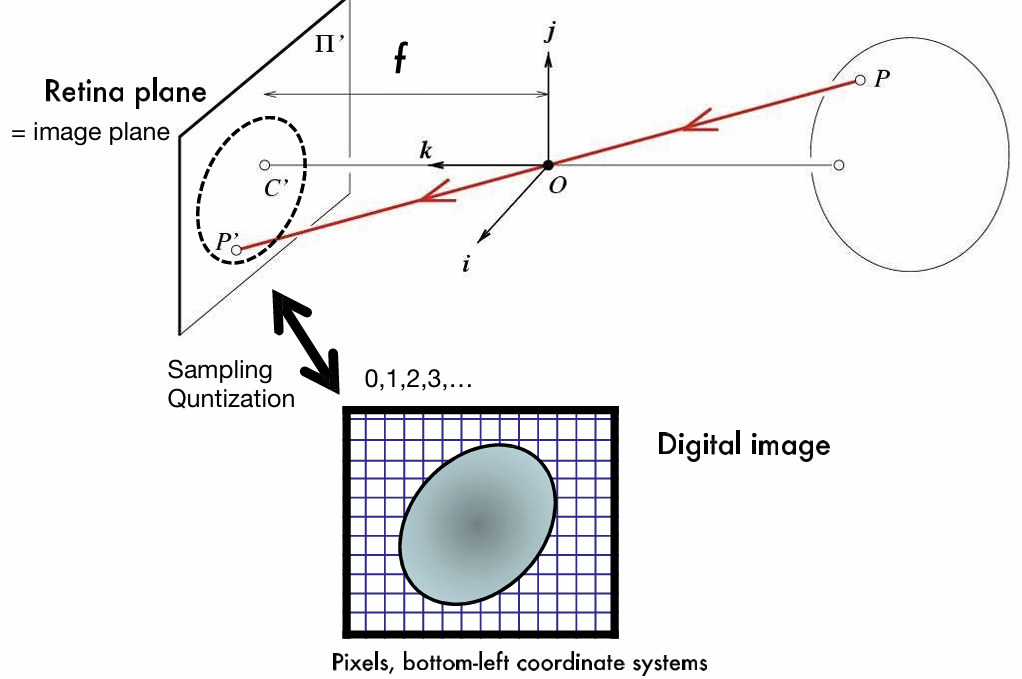
- Pinhole camera
- focus가 제대로 맞는 상태에서의 Image Plane
- From retina plane(Image plane) to images
- Sampling => Quntization
- Coordinate systems
1. Off set
- 원점을 맞춘다.2. From metrix to pixels
- 단위를 맞춘다. (metric 단위에서 pixel 단위로)- α = fk
- β = fl
=> 보통 k와 l은 같은 값 (정사각형 pixel)
Q) Is this projection transformation linear?최종 형태 A) linear하지 않아 matrix format으로 나타내기 어렵다. => Homogenuous coordinate를 이용하자!
- Homogeneous coordinate
- Projective 변환을 linear(선형)으로 표현하기 위해 사용하는 좌표계
- 2차원은 3차원으로, 3차원은 4차원으로
- 마지막 차원에는 "1"
==> linear system으로 표현하기 용이해진다.
- Eulcid => Homogeneous

- Homogeneous => Euclid

- Projective transformation in the homogeneous coordinate system
- x,y,z와 x',y'의 관계를 linear systme으로 나타낼 수 있다.
- Camera matrix
- Skewnes
- 가상의 Image plane과 camera sensor plane을 약간 틀어지게 놨다. (각도 Θ)
- Degrees of freedom of K
- 5 DOF (α, β, Cx, Cy, Θ)
=> 보통 α = β, Cx, Cy, (Θ는 잘 고려 안함) : 사실상 3개만 고려한다.
- Canonical projective transformation
- 기본형
- 2D
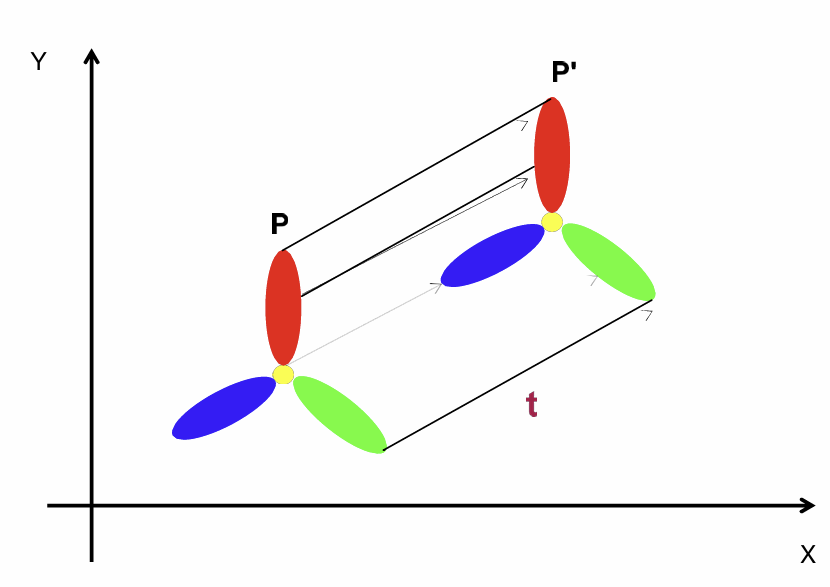
- 2D Translation
- 직선운동# DOF = 2
- 2D Scaling
- 크기 변환# DOF = 1
- 2D Rotation
- 중심 기준으로 회전# DOF = 1
- 2D Scale + Rotation + Translation
- 2D => 2D
- 3D
2D=>2D : 3x1=>3x1 matrix size 3x3
3D=>3D : 4x1=>4x1 matrix size 4x4
- 3D Translation
# DOF = 3
- 3D Rotation
# DOF = 3
- 3D Translation + Rotation
- World reference system
- Projective transformation
위에 식과 같은 식 # DOF = 11(5(I) + 6(E))
풀어쓰면 다음과 같다.
- Horizon line (= Vanishing line, line at infinity)
- Properties of projective transformation
- Euclidian으로는 표현 X
=> Homogeneous로 구별해서 표현 가능
- Projective camera
가장 단순화 version
투영 모델 종류
- Canonical Projective Transformation
- Weak Perspective Projection(= Para perspective)
- 객체가 멀고, 깊이 변화가 적은 경우 depth를 일정한 값(z0)으로 가정한다.
- 깊이에 따라 전체적으로 일정한 축소율로 투영된다.P,Q,R이 다 다른 위치에 있지만 같은 plane에 붙어 있는 것처럼 보인다.
# Perspective vs Weak perspective
Perspective vs Weak perspective - Perspective에서 맨 마지막만 0001로 바꾸면 Weak perspective
- Orthography (affine) projection
- z는 관계없이 다 버리고 x는 x로, y는 y로
- 카메라 중심과 이미지 평면이 무한히 멀리 있다고 가정
- 각 model들의 장단점
[Weak perspective]
- object가 멀리 떨어져 있는 것에 비래 작을 때(Scene이 작을 때) 계산하기 쉽다.
=> 제일 앞에 있는 나무와 제일 뒤에 있는 나무간의 거리가 카메라에서 나무들이 떨어져있는 거리에 비해 좁을때
=> 하나는 멀고 하나는 좁을 때 사용 X
[Pinhole perspective]
- 3D-to-2D mapping시에 더 정확하다.
'4-1 > 컴퓨터비전개론' 카테고리의 다른 글
| 6-2주차-Camera Calibration (0) | 2025.04.17 |
|---|---|
| 6-1주차-Camera Calibration (0) | 2025.04.17 |
| 4주차-Camera with Lenses (0) | 2025.04.16 |
| 3주차-Image Formation (0) | 2025.04.15 |
| 2주차-Math Basics (0) | 2025.04.14 |